1.2 벡터와 벡터공간
- 벡터의 개념과 위치 벡터
- 벡터의 내적
- 벡터들의 선형 결합
- 벡터공간
1. 벡터의 개념과 위치 벡터
정의 1.4. 크기(magnitude)와 방향(direction)을 가지는 양은 벡터(vector)라고 한다.

점 P에서 시작하여 점 Q에서 끝나는 것을 기호로 표현
점 P : 시점(initial point) , 점 Q : 종점(terminal point)

벡터의 크기
주어진 공간에서 점 P와 점 Q 사이의 거리
단위 벡터 (unit vector) : 크기가 1인 벡터
영벡터 (zero vector) : 크기가 0인 벡터

정의 1.5. 두 벡터가 놓인 위치에 상관없이, 크기와 방향이 같으면 '같은 벡터'라고 한다.
-> 한 벡터를 평행이동한 것은 모두 같은 벡터이다.
같은 벡터라는 것은 '다름'의 기준이 생겼다는 의미!
1. 크기가 같고 방향이 반대 (부호가 다름)
2. 벡터 v에 스칼라(실수) k 를 곱하여 벡터의 크기를 변화시킴
k : 양의 실수 -> 같은 방향
음의 실수 -> 다른 방향
v가 영벡터가 아닐 때,

벡터 v의 크기는 1이다. (단위벡터)
평행 벡터 : 두 벡터 v, w가 방향이 서로 같거나 반대이면, 다시 말해 두 벡터가 이루는 각이 0도 또는 180도이면 v와 w는 서로 평행이라고 하고 v//w 으로 표기한다.
+) 두 벡터가 평행일 필요충분조건은 한 벡터가 다른 벡터의 스칼라 곱인 것이다.
v//w <=> v = kw
정의 1.6. 벡터의 합(sum of vectors) : v + w는 v의 시점을 시점으로 w의 종점을 종점으로 하는 벡터


평행이동한 벡터는 모두 같다 -> v + w = w + v (교환법칙 성립)
+) 벡터의 차 : v - w = v + (- w)
w의 종점에서 v의 종점으로 가는 방향의 벡터

위치 벡터(position vector) : P의 좌표가 (a, b, c)이면 벡터 [a, b, c]
모든 벡터의 시점을 정해진 한 점에 기준으로 두기로 약속 (보통 원점을 기준으로 함)
v = [v1, v2, v3], w = [w1, w2, w3]라고 할 때,
v + w = [v1+w1, v2+w2, v3+w3]
kv = [kv1, kv2, kv3]
직교좌표계 R**3의 벡터 [x, y, z]의 크기는 원점 0에서 점 (x, y, z)까지의 거리

2. 벡터의 개념과 위치 벡터
정의 1.7. 두 벡터 v = [v1, v2, v3], w = [w1, w2, w3]에 대하여 v*w = v1w1 + v2w2 + v3w3를
두 벡터의 내적이라고 한다.
성질 : 교환법칙, 분배법칙, 스칼라곱, 자기자신 내적, 영벡터
Cauchy-Schwarz 부등식 (inequality)

*등호(=)는 v // w 일때만 성립 ( 두 벡터가 평행 + 필요충분조건 : w = tv (t는 실수)
정의 1.8. 정사영(projection) : 두 벡터 v, w와 두 벡터의 사잇각 θ에 대하여 실수값 ||v||cosθ 를 v의 w방향성분이라 한다.




벡터 v의 w방향 성분벡터
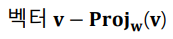
벡터 v의 w에 수직인 성분벡터
3. 벡터들의 선형 결합
- 선형결합 또는 일차결합 : R**n의 몇 개의 벡터들 v1, v2 ······ vn 에 대하여 c1v1 + c2c2 + ······· + cmvm 꼴로 표현된 벡터 (c1, c2, ····· , cm 은 스칼라)
정의 1.9. R**n의 벡터들 v1,v2, ····, vm에 대하여 만일 방적식 c1v1 + c2v2 + ···· +cmvm = 0 을 만족시키는 스칼라 계수가 c1 = c2 = ··· = cm = 0 뿐이면 벡터들 v1, v2, ··· ,vm 은 서로 일차독립(linearly independent)이라고 한다. 그렇지 않은 경우에는 벡터들 v1,v2, ····, vm은 서로 일차종속(linearly dependent)이라고 한다.
정리하자면 스칼라계수가 0이면 일차독립, 0이 아니면 일차종속
일차종속에서 '아니면'의 의미는 적어도 0이 아닌 스칼라 계수가 존재한다는 의미
(예제 1,5,) 주어진 R**3의 벡터들이 서로 일차독립인지, 일차종속인지 판정
a = [1,0,-1] b = [1,1,0] c = [1,0,1]
a를 c1 b를 c2 c를 c3
c1a + c2b + c3 = 0 을 만족하는 스칼라 계수가 0뿐인가?
[ (1) (2) (3) ] 각 자리에서 0이 아니라면 스칼라 계수에 곱해서 일차연립방정식을 만들어서 구해본다.
(1) a,b,c 전부 0이 아니기 때문에 전부 방정식에 들어감
c1 + c2 + c3 = 0
(2) b만 0이 아님
c2 = 0
(3) a는 -1, c =1
-c1 + c3 = 0
(1)(2)(3) 일차연립방정식의 해를 구하면 c1 = c2 = c3 = 0뿐이기 때문에 a, b ,c 는 서로 일차독립이다.
4. 벡터공간
벡터공간(vector space)
- 두 가지 연산으로 덧셈과 스칼라곱이 정의되어 있음
- 임의의 두 원소 v,w의 일차결합 cv + kw (c, k는 스칼라)이 다시 V의 원소
- 법칙 8가지 모두 만족
+) 법칙 8개 : 덧셈의 교화법칙, 덧셈의 결합법칙, 덧셈의 항등원, 덧셈의 역원, 스칼라곱의 분배법칙, 스칼라에 대한 벡터의 분배법칙, 스칼라곱의 결합법칙, 스칼라곱의 항등원
v + 0 = v (덧셈의 항등원)
v + (-v) = 0 (덧셈의 역원)
정의 1.10. 벡터공간 V에서 서로 일차독립이 되도록 할 수 있는 벡터들의 최대 개수를 V의 차원(dimension)이라고 부르고, 기호 dimV 로 나타낸다. 그리고 서로 일차독립인 벡터들의 최대 집합을 V의 기저(basis)라고 부른다.
- dimV : 기저에 속한 벡터의 개수
- 벡터공간 R**3에서 벡터들의 집합 B = {[1, 0, 0], [0, 1, 0], [0, 0, 1]}은 기저가 된다.
- 그 이유는 세 벡터는 서로 일차독립 + 여기에 어떤 벡터를 추가하더라도 더 이상 서로 일차독립이 아님.(이미 꽉 참)
- dim(R**3) = 3
- 표준정규직교기저 -> 정규직교는 벡터들의 크기가 1이며, 모두 서로 수직
정의 1.11. 벡터공간 V의 몇 개의 원소 v1,v2, ····, vm 에 대하여 이들의 모든 일차결합의 집합, 즉 {c1v1 + c2v2 + ··· + cmvm | c1,c2, ····, cm 은 스칼라} 를 이 벡터들의 생성공간(span)이라고 부르며, 기호 span{v1,v2,···,vm}로 나타낸다.
- 생성공간 자체도 벡터공간이 됨
- V의 원소들의 생성공간과 같이 자체적으로 벡터공간이 되는 부분집합을 부분공간이라고 부른다.
벡터공간 V의 부분집합 {v1, v2, ···· ,vm}이 V의 기저가 될 필요충분 조건
1. v1, v2, ····, vm은 서로 일차독립이다.
2. v1, v2, ····, vm가 벡터공간 V를 생성한다.
[공부하면서 참고한 블로그들]
https://blog.naver.com/ao9364/221542210272
벡터의 내적, 정사영으로 깊이 생각하기(개념편)
들어가기... 우리가 고등학교 수학 교과서에서 알 수 있는 정도로만 의미를 파악해 보면 다음과 같이 크게 ...
blog.naver.com
정사영 참고하기 좋음.
https://blog.naver.com/cindyvelyn/222111264182
벡터의 일차독립과 일차종속(Linearly independent, Linearly dependent) 그림으로 이해하기
벡터에 대해서가 아니더라도 어떤 두 대상 사이에서 독립과 종속이라는 용어는 둘의 관계성이 없거나 약할 ...
blog.naver.com
일차독립과 일차종속 이해하기
https://blog.naver.com/nilsine11202/221453109625
[선형대수] 0. 들어가며
데이터 분석 공부를 시작하면서 끊임 없이 들었던 이야기 중 하나는, 선형 대수가 머신러닝 공부의 가장 중...
blog.naver.com
이분의 요약도 잘 정리되어 있음 영상이 이해하는 데 도움이 된다.
https://blog.naver.com/ssooj/222505266230
기하 6. 평면벡터의 내적, 방향벡터와 법선벡터를 이용한 직선
기하 일곱 번째 개념 정리입니다. 오늘 정리한 개념은 '평면벡터의 내적'에 대한 내용이에요. 여...
blog.naver.com
기벡을 모르는 나에겐 그저 angel
'School Study > 2021-2' 카테고리의 다른 글
| [week 04] C++ 복습_3장 선택문 (2) (0) | 2021.10.16 |
|---|---|
| [week 03] C++ 복습_3장 선택문 (1) (0) | 2021.10.07 |
| [week 02] C++ 복습_2장 기본 프로그래밍 (0) | 2021.09.30 |
| [week 01] C++ 복습 (컴퓨터, 프로그래밍 및 C++ 입문) (0) | 2021.09.23 |
| [week 01] 미벡 기초 (데이터의 형식과 기본 연산) (0) | 2021.09.01 |



